Hegel’s most important philosophical work is the 1812 Science of Logic. While many agree about the importance of this work, little consensus exists regarding the subject matter or even the main topic of this book. Is the Science of Logic about logic? Is it some kind of metaphysical argument for the existence of God? Is it a theory of reality or a theory of thinking?
Hegel’s Logic is, first and foremost, a logic. The Science of Logic is a theory of thinking. Yet Hegel’s Logic is certainly not the kind of “logic” one might study in an introductory logic course within a philosophy department today. In fact, apart from Hegel’s brief treatment of judgments and syllogisms, very little of what is typically considered “logic” can be found within this text. What differentiates Hegel’s “dialectical logic” (or “speculative logic”) from “logic” in the usual sense?
A university logic course will typically teach “formal logic,” theories of validity, often using symbolic notation and demonstrations resembling mathematical proofs or calculations. Hegel, by contrast, understands logic in a much broader sense as a theory of thinking in general. Hegelian logic, accordingly, is not just a theory of formal validity, but offers what Kant called a “transcendental logic” or “system of pure reason,” that is, a systematic account of the categories and concepts that belong to philosophical cognition generally.
Formal Logic
“Formal logic” means logic understood as a theory of formal validity. By “validity,” logicians understand the formal principles that belong to good reasoning in general,
and this logical form is distinguished from the content of the arguments. When teaching students logic, we often use absurd arguments to help students differentiate between true and valid arguments. In my own lectures on logic, for example, I use the example “If pigs fly, then hell has frozen over. Pigs fly, therefore hell has frozen over” to illustrate modus ponens, a logical form. While there’s not any real connection between pigs flying and hell freezing over, this argument (however absurd) nevertheless corresponds to the logical form of modus ponens and is therefore valid, regardless of whether it says anything true or false.
Because formal logic merely concerns the logical forms of arguments and not the content of the propositions, we can express the different logical forms using symbolic notation. Modus ponens, for example, can be expressed as:
In this example, the “p” and “q” represent propositions, and this entire expression describes a specific formal structure that is valid within classical logic. By brute force, one can enumerate all of the formally valid logical structures within a particular system of logic, as well as all of those that are invalid. These formal structures can be examined independently of each other and have nothing to do with the meaning, truth, or falsity of propositions.
Hegel’s Critique of Formal Logic
In Hegel’s view, formal logic has its usefulness within specific disciplines, such as mathematics and law. Yet Hegel understands formal logic to be “spiritless” insofar as rather than resting on the content of concepts, the validity of propositions can be found simply by calculating the results that follow given a specific set of rules. Hegel compares this to the rules of a game, writing:
The deduction of the so-called rules and laws, of inference especially, is no better than the manipulation of rods of unequal lengths for sorting them out in groups according to size – than a children’s game of fitting together the pieces of a colored picture puzzle (SL, 32).
Today, the operations of formal logic can be done in a purely mechanical manner by a computer—just as a calculator can calculate mathematical sums.
Formal logic examines the different logical structures independently of each other, and often discovers these different logical forms in an almost empirical manner. The different logical forms do not necessarily have an intrinsic connection to each other, but are just all of the logical forms that happen to be present at hand in thinking.
In formal logic, the different logical forms are independent of each other and independent of the truth or falsity of the content. Hegel thus claims that these forms are “external” to each other and “external” to the content. They lack an “inner” connection to each other, a necessary connection where they can appear as part of an interconnected system.
Hegel’s Logic of Content
In Hegel’s Logic, logical form is not divorced from logical content. On the contrary, the logical form is itself the content. Dialectical logic is not just different from formal logic because it is paraconsistent (Aristotelian logic is also paraconsistent), but because it unfolds in a movement generated by the content of pure thinking itself. In each logical form, Hegel argues, something is thought and this thought has content that can be developed. By examining this content, Hegel can derive an interconnected system of categories in a linear progression.
The scope of Hegel’s logic is also wider than formal logic. Kant complained in the Critique of Pure Reason that formal logic “had not advanced a single step since Aristotle.” While this claim is perhaps unfair, since Kant was perhaps unaware of the tremendous wealth of work on logic in the middle ages, Kant nevertheless attempts to expand logic beyond a mere theory of formal validity into a theory of categories, that is a theory of the concepts that we must use to think about reality.
Hegel follows Kant’s precedent in seeing transcendental logic as having replaced metaphysics with logic. Hegel’s “Objective Logic,” accordingly, plays the role that was previously played by the area of metaphysics known as “ontology.” Yet Hegelian logic does not attempt to determine the nature of reality, but to unpack the conceptual content and limits of the thoughts we use when thinking about reality. Hegel does not, for example, propose that reality is composed of monads, but instead examines (for example) the thoughts that operate within a monadology, their points of tension, and the relation of these thoughts to human thinking as a whole.
How Dialectical Logic Works
Hegel’s logic is a logic of content, not a formal logic. The categories and logical forms, accordingly, are not assembled at random, but are shown to be necessarily connected to each other. We can understand this by looking at the opening of Hegel’s Logic.
The first categories in the logic are pure being and pure nothing. Hegel does not arrive at these categories by asking, empirically, what categories we happen to use to think about beings, but instead looks at the content of these thoughts in themselves. He does not ask about when these categories can be correctly applied to the world, but ask about what these pure thoughts themselves contain. What is the content of these thoughts?
If we examine pure being, a pure thought form, this pure thought contains its opposite as its content: pure being is pure nothing, since being can be said of everything, yet adds nothing to the thing, and it is only “pure” being if it is indeterminate. Since pure being abstracts from every sense of “being,” if we ask “what is being,” this implies that being could be determined as a being, yet as Heidegger famously pointed out, being is not a being. Since being has no content and is empty, being is “nothing.” Likewise, the thought of pure nothing contains no content, yet in thinking “pure nothing,” we nevertheless are thinking about nothing, meaning that nothing is in thought, which means that the thought of pure nothing contains pure being as its content.
The term “dialectic” (strictly speaking) refers to the way that categories (e.g. being and nothing) contradict themselves and turn into their opposites. Traditionally, this was used as a skeptical or sophistical procedure do deny knowledge or to investigate a realm of knowledge.
For Hegel, dialectic is just as much negative as positive. In the case of being and nothing, for example, the dialectical transition of each into their opposites allows us to arrive at a higher determination, that is, a more concrete thought. The higher thought is to recognize, not just that being and nothing are the same, but the thought of the transition of being into nothing and vice-versa. We thus arrive at the higher concept: Becoming.
Becoming cannot be one-sidedly determined as either something that is or is not because it is the state of transition between these extremes. Becoming—which is the first proper “concept” of the Logic—has its own content, insofar as we can think about becoming from two different sides. Becoming is both coming-to-be (the transition of nothing to being) and ceasing to be (the transition from being to nothing). We have thus moved to a higher, more determinate opposition. Each of these opposites, too, contain each other, and once coming-to-be ceases to be and ceasing to be comes to be, we arrive at Dasein or “determinate being,” the presence-at-hand of a determinate quality or absence of quality. This dialectical process continues until the entire system is complete.
Conclusion
The Hegelian dialectic examines the pure thoughts or categories of philosophy and, by peering into their definitions, discovers precisely how each of these categories becomes dialectical or self-contradictory and turns into their opposites.
Reading Hegel is so difficult because in order to grasp the logical transitions between categories, we must examine each of them as pure thoughts and understand how this thought content by its very definition contradicts itself and turns into its opposite. The procedure is similar to what Plato calls thinking the “it itself” or “idea/form itself,” yet unlike Plato, the “forms” (or pure thoughts) are not stable and self-same, but are part of a self-differentiating movement.
Hegel calls formal logic “spiritless” and “a calculus devoid of content” because the operations of formal logic can operate deductively and mechanically. Formal logic can operate deductively because it separates the formal validity of arguments from their content. Hegelian logic, by contrast, has to think about the content of logical categories and forms, to draw conclusions based on this conceptual content, and to ask—not just whether these categories and forms are valid—but whether they are true in-themselves.



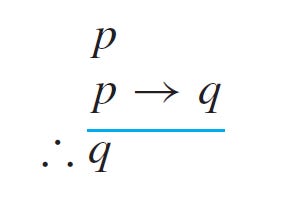
Thank you for this essay, such a clear and meaningful unpacking of Hegel’s dialectical logic. It really resonated with themes I’ve been exploring in my own writing, particularly around objectivity, coherence, and how truth unfolds in tension with contradiction.
I'd love to share ideas or dialogue sometime, your approach intersects deeply with some of the philosophical groundwork I’ve been developing. Feel free to take a look at my work if you're interested.
Appreciate your clarity and the depth of this piece.
Edit: I’m writing from more of a lay lens, but I’d really value the chance to share ideas. If you ever have a moment to glance at my work, I’d be honored to hear your thoughts.
Aristotle's logic is a relevance logic, but it is not paraconsistent. For Aristotle, the principle of non-contradiction is a metaphysical truth about reality.